Ja poste ruhig, wir haben das Thema in der schule zwar noch nicht angeschnitten deswegen tu ich mich da etwas hart, aber kann ja nicht schaden
An die Mathe Spezis:
-
-
Äh gute Frage!
Ne, so:
Delta ist ja klar oder? Dann aus dem c=3,2 ein Rechteck gemacht, also 2 mal die Höhe runtergezogen.Davon die Winkelhalbierende dann hat man ein 45° Winkel und kann damit über tan45°=h/c die höhe ausrechnen.
mitder Höhe kann man dann gamma ausrechen über cos gamma=h/b und damit ß!Hoffe verständlich, bin schon ein bischen müde!
-
Scheint ja richtig zu sein, weil die zeichnerische Lösung ja sehr viel dichter an deiner liegt.
Nur wat hab ick denn falsch gemacht ??????? Wo is mein Fehler, ick find keinen ?! -
Bei einem Quadrat sind die Winkelhalbierenden 45 Grad, aber nicht bei einem Rechteck.
-
Dat is wohl wahr!
Also is meins nur doch ned falsch?? Oder doch??? Oder doch nich??? :-k :-k :-r :-k
:-k :-r :-k  :-a
:-a 
-
Stimmt!!
ISt aber nahezu ein Quadrat!
Daher wahrscheinlich auch die bischen krummen zahlen!
Aber sonst kein Plan wie`s gehen soll!!
Peinlich, peinlich! -
Wahrscheinlich sind deswegen die kleinen Unterschiede zur zeichnerischen Lösung.
ABER WO IST MEIN FEHLER, ick find den ned ... :-aIck geh jetzt aus Frust, weil ick den Fehler ned finde, in die Badewanne!

-
Hehe keinen bock sowas zu rechnen!
Hinzeichnen und gut ist!
Ich werd jetzt erstmal schön Fussi gucken!

-
ich glaub ich versteh die aufgabe nicht...
wenn doch ist die lösung super billig ...
die höhe über die funkelsätze (nicht funktionen) berechnen , ebenso wie die teilwinkel in dem enstandenen dreieck, teilwinkel lassen sich immer auf die andere hälfte des trapezes (anders dreieck) übertragen. und schon kann man die seite d und was man sonst noch will berechnen...
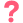
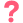
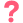
-
also, wo bekommst du den so aufgaben!
da fehlt ne angabe, da wette ich mit euch drum!
ausser zeichnerrischt ist das rechnerrisch fast nicht zu lösen!
fast, weil ich nen lösungsansatz hier habe, allerdings ist der nicht ohne. daher wollte ich erstmal abchecken, wie die GENAUE aufgabenstellung lautet!
-
Kann gut sein, dass der richtige Ansatz nicht ohne ist. Hab grad mit meiner Freundin geprochen. Ihre Schwester (Realschullehrerin) bekam das auch nicht raus. Also ich hab auch schon sher viele Ansätze versucht. Morgen weiß ich mehr. Aber für eine Aufgabe der 10. Klasse schon ein bißchen heftig. Hatte immerhin Mathe LK und so auf die schnelle ist das irgendwie nicht rechnerisch zu lösen.
-
also, in mit meinem schulmathe, naja, da war ich immer saugut, und an der uni weht en anderer wind, naja wie dem auch sei, ich hab en momentchen gebraucht,
ich geb dir mal meinen ansatz:
1) h^2+y^2=16 ---> h = 16-y^2
2) x^2+h^2=d^2
3) x+y=3,8mit X= teilstück unten links, und y teilstück unten rechts, womit x= 7-3.2 -y eben so für Y mit X
ansatz--> 1)-->2)
und schon hast du nach kurzem gezícke nur noch X in deiner gleichung stehen,
x^2 +16-y^2=d^2 mit cos72=x/d ---> d=x/cos72
alles weitere ist nur noch gerechne, damit dürftest du alles rausbekommen!
-
Jo,
Also habs nochmal nachgerechnet, auf den Ansatz bin ich noch gar nicht gekommen, hab immer viel komplizierter gedacht .
.
Kann ich gut nachvollziehen 1) u 2) Phythagoras 3) 7-3,2=x+y.
Bekomm da jetzt für h ~ 1,66 x ~ 0,162 y ~ 3,638 d ~ 1,67 -
Bei der Probe stimmt dann Alpha aber nicht mehr.
Alpha = arccos ( x/d ) = 84,4° , soll aber 72° sein :-k -
Ganz einfach mit dem Strahlensatz beginnen.
Zuerst die beiden schrägen Seiten nach oben in einen Schnittpunkt verlängern. Dann verhält sich 7/3,2 wie 4/(4+x) So kann man dann nach x umstellen und erhält 3,36842 cm, Damit habe ich über dem Trapetz ein Dreieck mit 2 bekannten Seiten und einem bekannten Winkel. Jetzt kommt der Sinussatz. Der besagt daß sich sin72 / 3,36842 verhält wie sin d/ 3,2. usw usw und dann erhalte ich das Stück über der gesuchten Trapetzseite zu 2,432cm. Jetzt wieder Strahlensatz 7/(?+2,432) ist wie 3,2 /2,432 und damit ist ?=2,889cm. -
Zitat
Original von TiGaer
ich glaub ich versteh die aufgabe nicht...wenn doch ist die lösung super billig ...
die höhe über die winkelsätze (nicht funktionen) berechnen , ebenso wie die teilwinkel in dem enstandenen dreieck, teilwinkel lassen sich immer auf die andere hälfte des trapezes (anders dreieck) übertragen. und schon kann man die seite d und was man sonst noch will berechnen...
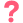
was ist denn nun damit
-
Womit? Und was sind Funkelsätze?
-
winkel natürlich...

-
Trivialgeometrie

Aber man kann ganz schön blöd schauen am Anfang.
Also zuerst "schneidet" man das rechteckige Mittelstück mal raus.
Dann haben wir ein Dreieck mit einem Winkel und 2 bekannten Seiten
Dann noch ein wenig mit dem Sinussatz hantiert und siehe da: X=2,889cm -
hallo ??? hab ich doch gestern abend schon so gesagt... konnte mir bloß wirklich nicht vorstellen das da keiner drauf kommt...
Jetzt mitmachen!
Sie haben noch kein Benutzerkonto auf unserer Seite? Registrieren Sie sich kostenlos und nehmen Sie an unserer Community teil!
